Вывод приближённой формулы
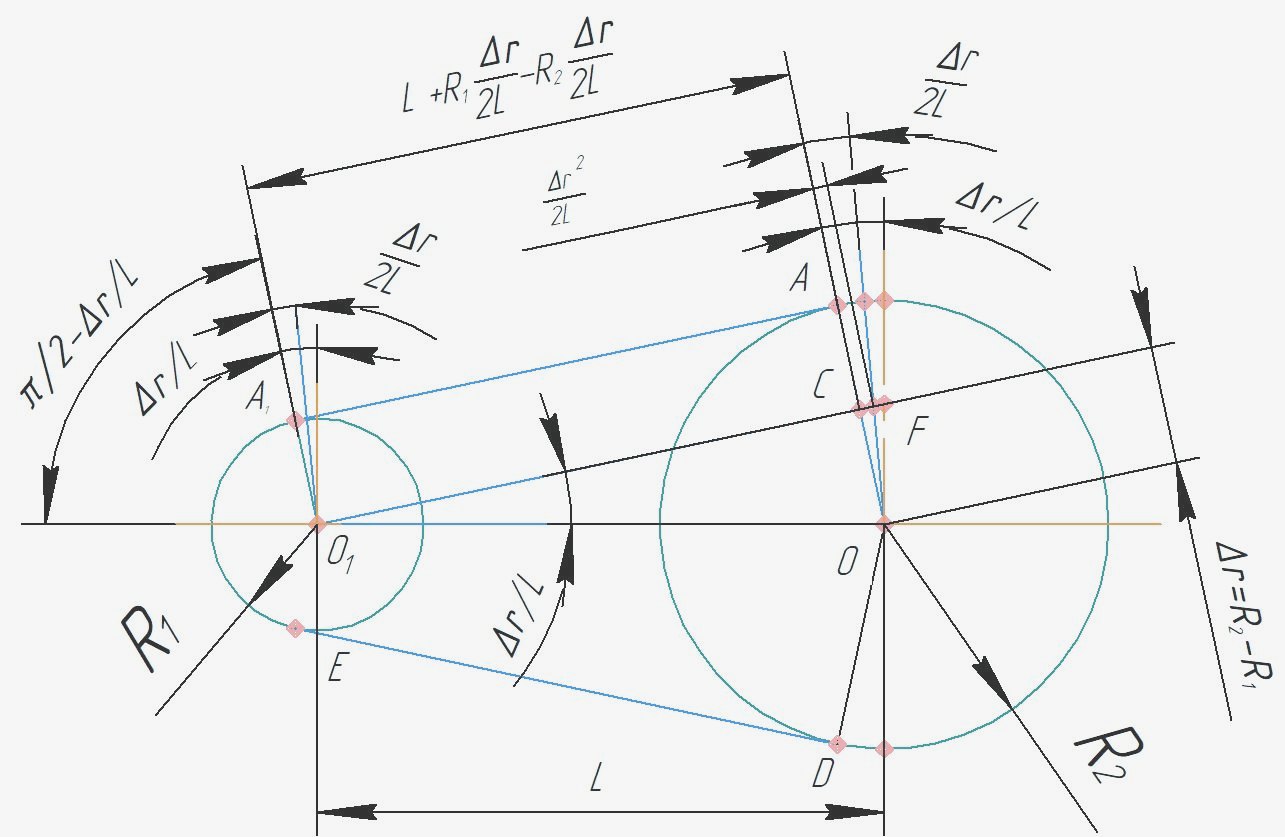
Рассмотрим вывод приближённой формулы. Если угол \widehat{СO_1O} небольшой, то синус малого угла можно численно приравнять к самому углу в радианах. Погрешность, если угол не превышает 30° менее 4%.
Арккосинус угла получаем из свойств прямоугольного треугольника:
Преобразуем формулу (2). Длина дуги, огибаемая пассиком на большом шкиве:
Преобразуем формулу (3). Длина дуги, огибаемая пассиком на малом шкиве:
Длина касательных выходит из равнобедренного треугольника \widehat{FO_1O}, где дуга окружности радиусом ∆r, отсекаемой биссектрисой, примерно равна лишнему отрезку |CF|:
Учитывая приближения (15, 16, 17), эквивалент формулы (5) - общая длина пути пассика:
Упрощаем:
Переходим к диаметрам. Длина и полудлина пассика натянутого на шкивы:
Уравнения (20, 21) выражают длину и полудлину пассика надетого на шкивы и являются приближёнными, при условии, что расстояние (L) между осями шкивов больше суммы их радиусов L>\frac{1}{2}\left( d_2+d_1 \right). Ниже ссылка на онлайн расчёт пассика по точной формуле (12) с коэффициентом натяжения. Для сравнения формул (12) и (20, 21), установите в программе расчёта коэффициент натяжения (k = 1) равным единице. Коэффициент натяжения - это отношение длин (полудлин) натянутого на шкивы к свободному пассику. На практике последнее слагаемое в уравнениях (20, 21) можно исключить из-за его незначительности. По сути, мы находим средний диаметр, вычисляем длину окружности и прибавляем двойное расстояние между шкивами. В результате формулы (20, 21) упрощаются:
Copyright©Aleksei Tarasov (2021)