Битность магнитной записи

История этой работы тянется из просторов современного интернета в ностальгию по магнитной записи прошлого века. Наткнулся как-то у себя в загашнике на стопку старых кассет, пролежавших без надобности много лет. Решено было достать старый Шарп, неплохо сохранивший свой облик, протереть головки одеколоном и включить «воспоминания». Да, завис я на несколько часов, гоняя туда-сюда старые записи. Нахлынувшая ностальгия вопросительным образом образовала в моём пытливом мозгу нетривиальный вопрос – у тебя же есть интернет, где вся музыка собрана, да ещё под неё кто-то рот открывает, зачем тебе этот старый хлам? Ну… да, полез в глобальную сеть, оказывается, целые музеи магнитофонов у людей. Собраны огромные коллекции, достойные бывших «Берёзок» и «Комиссионок». Сверкающие на полках Сони, Панасоники и Шарпы басовитыми мелодиями наполняли пространство вокруг “коллекционера”. Наверно и эта сфера деятельности не так уж бесполезна, подумал я, к тому же редкие модели можно с уверенностью возвести в ранг произведения искусства, этакую вершину дизайнерской мысли прошлого. Хвалебные оды “аналоговой записи” можно увидеть в постах и на форумах, посвящённых магнитофонам. Тем самым, рынок магнитофонов продолжает жить. Когда-то я принимал участие в разработках подобной техники на закате магнитофоностроения, их схемотехника мне неплохо знакома. Но возникает стойкое ощущение, что это просто ностальгия, а нас дурят, впаривая натёртые до звенящего блеска “трубы от граммофонов”, убаюкивая воспоминаниями о светлом прошлом. Так или иначе, решил я выяснить, насколько же аналоговая запись действительно является аналоговой? Сама теория на грани фола, но рабочая. Некоторые подробности я опустил, сокращая количество формул и взрыв мозга. Кому не интересны формулы и подробности технического характера, мотайте сразу в конец работы – на вывод.

Представим амплитуду как произвольную функцию по времени, тогда функция амплитуды:

A=f(t) \tag{1}

Рассмотрим произвольно меняющийся сигнал (Рис.1), и выделим из него участок времени ∆t, который имеет размерность времени квантования цифрового сигнала, мы не будем сейчас вникать в индивидуальность этого участка, т.к. это может быть любой квант сигнала.

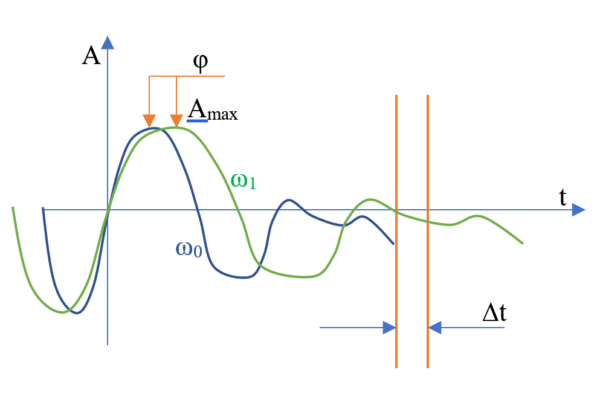
Рисунок 1. График разницы частот

Если ∆t будет настолько мало, что отсечённый на функции отрезок можно принять за линейный, тогда график функции (Рис.1) на этом участке имеет:

1. Возрастание; 2. Убывание; 3. Горизонтальный участок.

Отношение наклонов характеристик двух соседних участков функции не могут превышать некоторой константы, потому что частотный диапазон тракта записи-воспроизведения ограничен сверху техническими возможностями. Ограничение частотного диапазона снизу даёт нам так же невозможность длительного существования участка (3). По своей сути, наклон характеристики – это производная функции в точке (A,t) нашего графика. Максимально возможный наклон характеристики определён максимально возможным значением частоты тракта записи-воспроизведения, назовём её как $(ω_{max})$ . Для тракта записи-воспроизведения минимальная амплитуда сигнала соответствует булевой функции единичного скачка сигнала:

\begin{matrix} |A_{min}|&=&\left\{ \begin{matrix} logical (1), &if (A = A_{min}) \\ logical (0), &if (A \le A_{min}) \end{matrix} \right. \end{matrix} \tag{2}

Модуль амплитуды указывает на толерантность положительной и отрицательной полуволн. Тогда, максимальную амплитуду мы можем представить в виде суммы минимальных скачков:

|A_{max}|=n|A_{min}| \tag{3}

Значения смещения фазы (φ) пика сигнала $(A_{max})$ в точке $(\pi)$ , двух близких частот, различаются проявлением единичного сигнала (бита), который появляется при меньшей частоте. Так как амплитуда $(A_{max})$ одна и та же, то функция единичной амплитуды синусоидального сигнала для более высокой частоты, отстаёт на угол (φ). Амплитуда единичного скачка сигнала:

A_{(1)}=A_{max} \sin{(\omega_1 t)}= A_{max} \sin{(\omega_{max}t)} = logical(1) \tag{4}

Данная формула очень замечательна, какую бы амплитуду $(A_{max} \ge A_{min} )$ мы не попытались записать на максимальной частоте $(\omega_{max})$ , на выходе будет только одно значение, равное одному биту сигнала, так как предельная частота изначально принята минимальному уровню сигнала на выходе тракта записи-воспроизведения:

A_{(0)}=A_{max} \sin{(\omega_0 t)}= A_{max} \sin{(\omega_{lim}t)} = 0 = logical(0) \tag{5}

Определим дельту частот, как модуль разницы предельной, при которой амплитуда записи сигнала не отличима от шума звукового тракта и ленты, и максимальной, проявляющей стабильный бит:

\Delta \omega = |ω_0 – ω_1| \tag{6}

Определяем амплитуду битовой ступени:

A_{(1)} = A_{max} \sin{(\omega_0 t -\omega_1 t)} \tag{7}

Так как частоты, при которых образуется бит информации аналогового сигнала близкие, то временные точки приблизительно равны, второе условие (Ф.2) определяет равновозможный вариант записи нулевого и единичного бита. Выводим предельную частоту:

\omega_0 t = \omega_1 t + asin{\frac{|A_{min}|}{|A_{max}|}} \tag{8}

f_{lim} = \frac{\omega_1}{2 \pi} + \frac{asin{\frac{|A_{min}|}{|A_{max}|}}}{2 \pi t} \tag{9}

Из графика шумовой составляющей выделяем два участка, один с максимальной частотой, второй с минимальным изменением амплитуды сигнала из пологого участка кривой, получаем данные для вычислений. Участок измерения частоты выбран длительностью 500 мкс. Это порог реакции слуха на изменение фронта атаки, или спада сигнала. Теория основана на характеристиках слухового органа. Для стирания ленты, магнитофон переведён в режим $CrO_2$ (оксида хрома), так как стирающий ток больше. Запись максимального сигнала производилась с использованием простейшего генератора-программы на основе звуковой карты компьютера собственной разработки (будет выложен на сайте). В качестве измерительной системы сначала был использован аналоговый осциллограф, но как оказалось, программныммный способ измерения звуковых характеристик магнитофона выдаёт аналогичные результаты. Звуковая карта с 24 битным АЦП полностью перекрывает потребности в подобных измерениях.

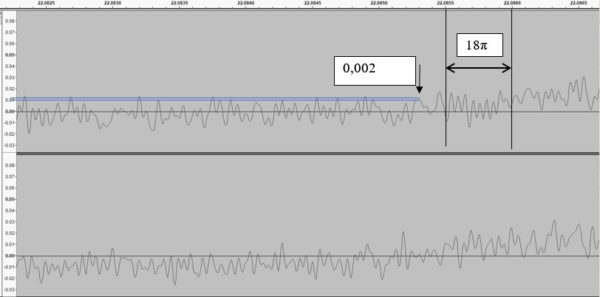
График шума стёртой ленты

Из графика шумов и максимальной амплитуды подопытного Шарпа получаем предельную частоту:

\frac{asin{\frac{0,002}{0,9}}}{2 \pi 0,0005} + \frac{18 \pi}{2 \pi 0,0005} \approx 18kHz \tag{10}

Необходимо отметить, что мы не привязываемся к стандартам, а ищем практический результат, на основе которого описываем цифровое преобразование, в том числе и на минимальных уровнях сигнала, где частота записи максимально возможна. Так же отметим, что амплитудой мы оперируем в условных единицах (у.е.). Уровень громкости не меняется при измерениях, а нагрузкой служит активное номинальное сопротивление. Частота дискретизации одного канала Шарпа должна быть выше второй гармоники предельной частоты воспроизведения, а звуковой тракт обеспечен фильтром низких частот, который в схемотехнике магнитофона присутствует:

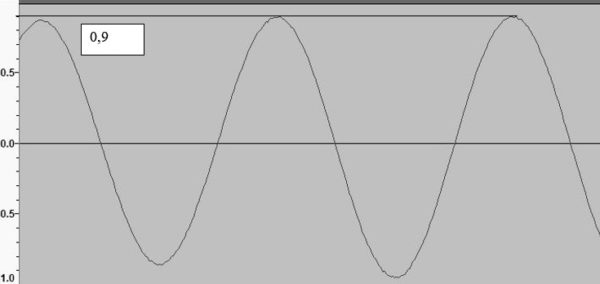
f_{sampling} = 2 f_{lim} = 2 \cdot 18kHz = 36kHz \tag{11}

График максимальной амплитуды

Динамический диапазон ограничен сверху перегрузочной способностью ленты. Усилители записи снабжены ограничителями уровня, которые предотвращают перегрузку ленты. Определяем Битность аналогового тракта, как:

N_{bit} =log_2 \left ( \frac{2|A_{max} - A_{min}|}{|A_{min}|} \right ) \approx log_2 \left ( 2 \frac{|A_{max}|}{|A_{min}|} \right ) \tag{12}

Двойка – это размах амплитуд. Компадерные шумоподавители могут расширить динамический диапазон, это зависит только от схемотехники аппаратов. Увеличивая амплитуду битовой ступеньки $(A_{min}),$ компандер-экспандер увеличивает динамический диапазон, но теряет качество. Кстати, характерные искажения систем шумопонижения являются следствием увеличения амплитуды битовой ступеньки. Впрочем, это был компромисс, между качеством и шумом. Так же, к этому моменту относятся и системы динамического подмагничивания, которые увеличивали способность записи на высоких частотах. Большую часть искажений привносила несовершенная механика магнитофона, система лента-головка, коммутация, схемотехника предварительных каскадов, а так же плохо спроектированные источники питания. На самом деле я не оговорился, качественная система питания может быть материально дорогой. Для магниточувствительных элементов требовалась хорошая компоновка блоков, система экранов, расположение общих точек и сама схемотехника. Я так же понимаю, что воспроизвести с помощью цифры аналоговый сигнал потребует высоких частот преобразования. На примере исследования магнитной записи явно видно, что сигнал на выходе "аналогового" магнитофона так же не является в полной мере аналоговым, так как зависит от шумового квантования, а его нестабильность вызывает дополнительную потерю чёткости звуковой картины, что несопоставимо даже с бюджетными ЦАП! Итак, момент истины:

N_{bit} =log_2 \left ( 2 \cdot \frac{0,9}{0,002} \right ) = 10 bit!

Вывод

Даже со значительными поблажками, настоящая “битность” кассетного магнитофона составляет 10 бит, при частоте дискретизации 36кГц. Ни о каком превосходящем качестве, в сравнении с цифрой 16 – 24 бита, не может быть и речи. Магнитная запись – технология ушедшая, больше интересна коллекционерам «блестящих аппаратов», а качество звука является субъективной эмоциональной оценкой. Можно также сделать вывод о неспособности ленты переносить сигналы с битовой глубиной превосходящей уровень отношения сигнал/шум. Паразитная флуктуация приводит к провалу разборчивости фонограммы – ухудшению её прозрачности по сравнению с цифровым носителем. Для уверенности были произведены пробные записи эталонной фонограммы в высоком разрешении на кассету и в ухудшенном (10 бит 36 кГц) цифровом формате. При прослушивании наблюдалась поразительная близость качества звучания этих фонограмм.